Hyperparameter Optimization

This project aims at optimizing the hyperparameters of models learned by minimizing nonsmooth functionals

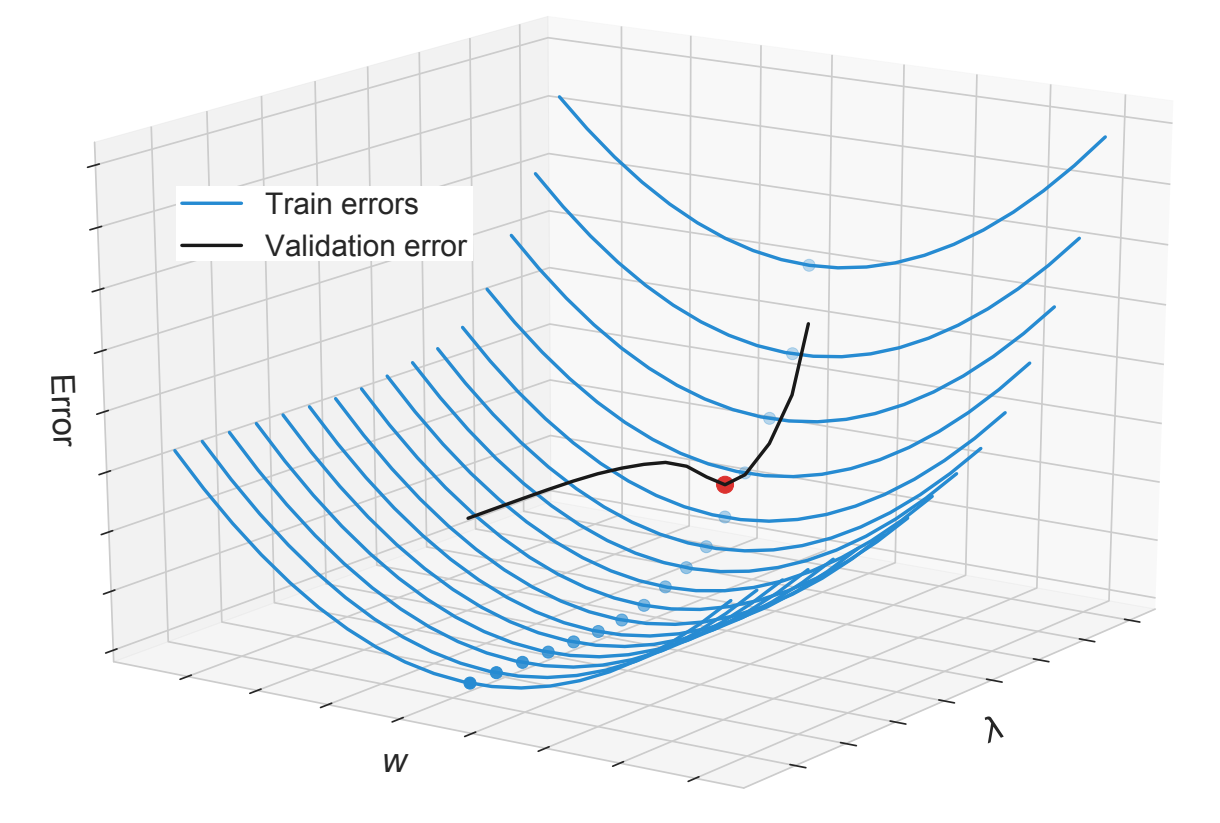
preview

Image Credit: Franceschi, L., et al. “Bilevel programming for hyperparameter optimization and meta-learning.” (2018).

With recent technological advances, high-dimensional datasets have become massively widespread in numerous applications ranging from social sciences to computational biology. In addition, in many statistical problems, the number of unknown parameters can be significantly larger than the number of data samples, thus leading to underdetermined and computationally intractable problems. In order to select the relevant parameters, a lot of work has been devoted to sparsity-inducing norms, thus resulting in non-smooth optimization problems. Note that since these problems are nonsmooth, the corresponding solvers are usually nonsmooth as well.

Besides the design of efficient solvers, these models also require to tune many (sometimes thousands of) hyperparameters whose value strongly affect the quality of the solution. As such, a simple grid search quickly becomes out of hand.

The principal contributions of this project are i) the design of smooth algorithms for non-smooth optimization problems and ii) the formulation of the hyperparameter learning problem as a continuous bilevel optimization problem where:

  • the lower-level problem computes the solution given the hyperparameters
  • the upper-level problem aims at tuning the hyperparameters so that the lower-level solution is optimal in some sense (e.g., lower validation error, sparser representation)

    • Related Publications

    1. M. De Santis, J. Frecon, F. Rinaldi, S. Salzo, M. Schmidt and S. Venturini,
      Relax and Penalize - a New Bilevel Approach to Mixed-Binary Hyperparameter Optimization,
      Under review, 2024.
      Article Page   PDF   BibTeX  
    2. J. Frecon, R. Grazzi, S. Salzo and M. Pontil,
      Smooth optimization of orthogonal wavelet basis,
      Conférence sur l'Apprentissage Automatique (CAp), 2021.
      Article Page   PDF   BibTeX  
    3. J. Frecon, S. Salzo, and M. Pontil,
      Unveiling Groups of Related Tasks in Multi-Tasks Learning,
      International Conference on Pattern Recognition (ICPR), 2020.
      Article Page   PDF   BibTeX  
    4. J. Frecon, S. Salzo, and M. Pontil,
      Bilevel learning of the group Lasso structure,
      Conference on Neural Information Processing Systems (NeurIPS), 2018.
      Article Page   PDF   BibTeX   Toolbox  
    5. J. Frecon, S. Salzo, and M. Pontil,
      Inferring the group Lasso structure via bilevel optimization,
      ICML Workshop - Modern Trends in Nonconvex Optimization for Machine Learning, 2018.
      Article Page   PDF   BibTeX   Toolbox  

    Back