Multivariate Scale Invariance

Joint analysis of the scale invariance of multivariate data.

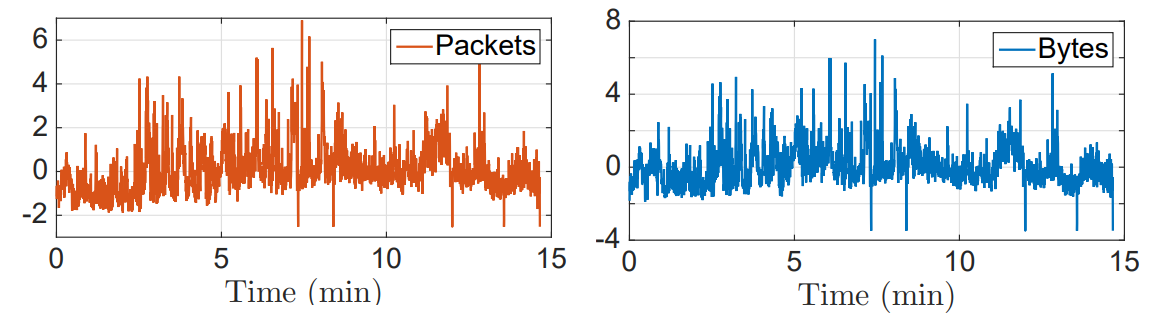
preview

Example of aggregated packet and byte aggregated time series from the MAWI repository

Scale invariance, or scaling, is now recognized as an ubiquitous property in a variety of real-world applications which are very different in nature. The so-named scale invariance paradigm is based on the assumption that temporal dynamics in data are not driven by one, or a few, representative time scales, but by a large continuum of them. Self-similar stochastic processes provide the basal mathematical framework for the modeling of scaling phenomena. In essence, self-similarity states that a signal cannot be distinguished from any of its dilated copies. Fractional Brownian motion (fBm) - the only Gaussian, self-similar, stationary increment process – has massively been used as a reference process in the modeling of scaling properties in univariate real-world signals.

Notwithstanding its theoretical and practical importance, fBm falls short of providing an encompassing modeling framework for scaling because most modern contexts of application involve the recording of multivariate time series that hence need to be jointly analyzed. The construction of a comprehensive multivariate estimation paradigm is still an open problem in the literature. The so-named Operator fractional Brownian motion (OfBm) is a natural extension of fBm. It was recently been defined as the only Gaussian, multivariate self-similar process with stationary increment.

In this project, our contribution is three-fold.

  • First, the full identification of bivariate OfBm is formulated as a non-linear wavelet domain regression problem.
  • Second, an algorithmic solution for the associated optimization problem is devised by means of a Branch & Bound procedure, which is essential in view of the highly non-convex nature of the latter.
  • Third, an application to anomaly detection in internet traffic is then constructed based on OfBm parameters estimated from bytes and packets time series.

    • Related Publications

    1. J. Frecon, R. Fontugne, G. Didier, N. Pustelnik, K. Fukuda and P. Abry,
      Non-linear Regression for Bivariate Sef-similarity Identification - Application to Anomaly Detection in Internet Traffic Based on a Joint Scaling Analysis of Packet and Byte Counts,
      International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016.
      Article Page   PDF   BibTeX   Toolbox  
    2. J. Frecon, G. Didier, N. Pustelnik and P. Abry,
      Non-Linear Wavelet Regression and Branch and Bound Optimization for the Full Identification of Bivariate Operator Fractional Brownian Motion,
      IEEE Transactions on Signal Processing, 2016.
      Article Page   PDF   BibTeX   Toolbox  

    Back