Physics-Guided Machine Learning

01 March 2023 - less than 1 min read time
Tags: Neural Network PDE

Work in progress

In what follows, we distinguish two cases wether the PDE describing the underlying dynamic is known or not.

1. Models

PINNs [Raissi et al., 2018] PDE-known. This paper first introduced the concept of Physics-Informed Neural Networks (PINNs). Instead of resorting to numerical PDE solvers, the originality of this work is to train a neural network to predict the solution of a known PDE at any spatio-temporal point. More formally, it relies on a neural network \(f_\theta\), with parameters \(\theta\), whose goal is to map \([x,t]\) to the solution \(u([x,t])\) of the PDE at \([x,t]\). The parameters \(\theta\) are trained so that three conditions are met:

In practice, \(\ell_2^2\) residuals (i.e., MSEs) are computed on some pre-defined spatio-temporal points to quantify, to what extents, each of the condition is satisfied. As such, \(\theta\) is found so that the sum of \(\mathcal{L}_{\rm PDE}\), \(\mathcal{L}_{\rm BC}\) and \(\mathcal{L}_{\rm IC}\) is minimized

APHYNITY [Yin et al., 2021] PDE-partly-known.

FNO [Li et al., 2021] PDE-unknown. Fourier Neural Operators (FNO)

2. Meta-Learning

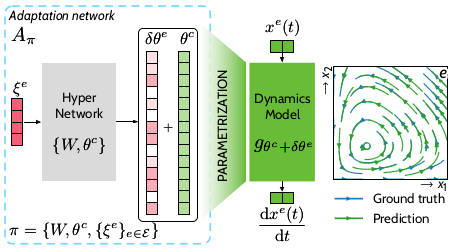
CoDA [Kirchmeyer et al., 2022] PDE-unknown. The COntext-informed Dynamics Adaptation (CoDA) method …

References